최근 인과추론(Causal Inference)이라는 분야에 대해 관심을 가지게 되서 인과추론에 대해 자세히 설명해놓은 자료인 <Causal Inference for The Brave and True>을 정리하고자 한다.
앞서 통계적인 언어가 많이 나와서 한번에 정리하고 글을 시작한다.
- ITE: 개별 처치 효과
- 실험 대상 i에 처치가 결과에 미치는 영향을 의미
- $ITE = Y_i(1) - Y_i(0)$
- ATE, (Average Treatment Effect): 평균 처치 효과
- 개별 처치 효과에 대한 평균
- $ATE = E[Y_1 - Y_0]$
- ATET/ATT(Average Treatment Effect on the treated): 처치받은 그룹에 대한 평균 처치 효과
- $ATT = E[Y_1 - Y_0|T = 1]$
- ex) T = 1인 그룹에 대한 ITE 평균
Machine Learning(상관관계) vs Causal Inference(인과관계)
"연관은 인과관계가 아니다."
머신러닝은 Task를 예측 문제로 프레임화하여 예측을 수행한다.
데이터만 제대로 준비되어 있다면 다양한 바운더리에서 예측을 수행할 수 있다.
그러나, 머신러닝은 데이터가 모델에 적합된 것과 조금 다를 경우 제대로 작동하지 않으며, 인과관계 유형의 문제를 잘 다루지 못한다.
인과추론의 문제는 '만약에 ~'라는 질문에 답할 것을 요구한다.
예를 들어 "현재 상품에 대해 요청한 가격을 사용하면 어떻게 될까?"와 같은 질문말이다. 그리고 이러한 질문에는 우리가 답을 알고자 하는 인과적인 질문이 포함되어 있다. 우리는 이러한 인과관계 질문에 대해 끊임없이 대답해야하지만, 머신러닝의 경우 상관관계 유형 예측에 의존하여 인과추론의 문제를 해결할 수 없다.
앞으로 나올 내용은 연관성을 인과관계로 만드는 방법을 알아내는 데 포커스를 둔다.
When Association IS Causation
직관적으로 우리는 연관성이 인과관계가 아닌 이유를 알고 있다.
예를 들어, 학생들에게 태블릿 PC를 제공하는 학교가 그렇지 않은 학교보다 더 나은 성과를 보이면, 태블릿을 제공하는 학교가 제정적으로 더 부유한 사실은 알 수 있을 것이다. 때문에, 해당 학생들은 테블릿이 없이도 평균보다 더 잘 할 수 있을 것이다(연관성). 그러나 수업 시간에 아이들에게 태블릿을 제공하는 것이 아이들의 학업 성취도를 높일 것이라고 결론지을 수 없다(인과관계).

이제 이것을 수식으로 증명해보자. 아래는 표기법에 관한 내용이다.
Treatment(처리)
$T_i$는 실험대상 i에 대한 Treatment를 나타낸다. 여기서의 처치는 효과를 알고자 하는 일부 개입을 나타내는데 사용할 용어라고 이해하면 된다. (위의 예시에서는 태블릿 유무가 T가 됨, 간혹 T대신 D라고 표기되기도 함!)

Outcome Variable(결과 변수)
다음은 실험대상 i에 대해 관찰된 결과 변수를 $Y_i$로 정의한다. 결과는 우리가 관심이 있는 변수로 처치(Treatment)가 결과에 영향을 미치는지 알고 싶은 대상이다. (위의 예시에서는 학업 성취가 결과 변수가 됨)
인과적 추론의 근본적인 문제는 Treatment가 있든 없든 같은 실험 대상에 대해 (다른 처치에 대해) 동시에 관찰할 수 없다는 것이다.
Potential Outcomes(잠재적 결과)
그 다음은 잠재적 결과(Potential outcomes)로 실제로 일어나지 않았으나 발생할 수 있는 결과를 의미한다. 대신 Treatment를 받은 경우, 무슨 일이 일어날지를 나타낸다. 일어난 잠재적 결과를 사실(factual)이라고 부르고 일어나지 않은 결과를 반사실(counterfactual)이라고 부른다.

이는 $Y_i(t)$로도 표현할 수 있음에 주의하자.
위의 예시로 표현하자면, $Y_i(1)$는 태블릿이 있는 교실에 있는 경우 학생 i에 대한 학업 성취도를 나타내고, 학생 i가 태블릿을 받지 못한 경우엔 $Y_i(0)$의 학업 성취도를 관찰할 수 있다. 만약 학생 i가 태블릿을 받았다면, $Y_i(1)$를 관찰할 수 있지만, 태블릿을 받지 못한 경우 $Y_i(1)$은 정의되어 있지만 우리가 관측할 수 없다. 이를 반사실적 잠재적 결과(counterfactural potential outcome)라고 한다.
ITE(개별 처치 효과, Individual Treatement Effect)
Potential outcomes를 통해 개별 처치 효과(ITE)를 정의할 수 있게 된다. 개별 처치효과는 실험 대상 i에 처치가 결과에 미치는 영향을 의미한다.
$$ITE = Y_i(1) - Y_i(0)$$
인과추론의 근본적인 문제로 잠재적 결과 중 하나만 관찰할 수 있기 때문에, 추정하기 더 쉬운 평균 처치 효과(ATE, Average Treatment Effect)가 더 많이 사용된다.
$$ATE = E[Y_1 - Y_0]$$
이보다 조금 더 추정하기 쉬운 값은 처치받은 그룹에 대한 평균 처치 효과(ATET/ATT, Average Treatment Effect on the treated)다.
$$ATT = E[Y_1 - Y_0|T = 1]$$
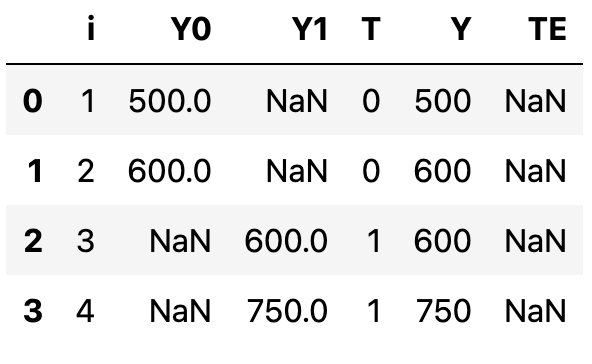
아래 계산 예시를 들어보자. 아래와 같은 데이터가 존재한다고 가정해보자.

ATE는 개별 처치 효과(마지막 열)에 대한 평균을 의미한다.
$$ATE = (-50 + 0 - 200 + 50)/4 = -50$$
이를 해석하면 태블릿이 학생들의 학업 성취도를 평균적으로 50점 감소시켰음을 의미한다.
ATT는 T = 1일 때, 개별 처치 효과에 대한 평균이다.
$$ATT = (-200 + 50)/2 = -75$$
즉 이를 해석하면 태블릿이 학생들의 학업 성취도를 평균적으로 75점 감소시켰음을 의미한다.
그러나 우리가 실제로 마주할 데이터는 아래와 같으며, 전과 같이 ATE를 계산하게 된다면, 연관성을 인과관계로 착각하는 실수를 저지르게 되는 것이다. 이는 인과추론에서 가장 중요한 Bias와 관련이 있다.
★ Bias(편향)
Bias는 연관성을 인과관계와 다르게 만든다.
결론부터 말하자면 Bias는 실험군과 대조군이 처치를 받지 않은 경우, 처치 전에 실험군과 대조군이 어떻게 다른지를 나타낸다. 예를 들어, $E[Y_0|T=0] < E[Y_0|T=1]$를 보면 태블릿 제공 여부와 무관하게 학생들에게 태블릿을 줄 수 있는 학교가 그렇지 않은 학교보다 낫다고 생각할 것이다.
이는 우리가 통제할 수 없는 많은 변수인 교란변수(Confounding variable)이 Treatment와 함께 바꾸기 때문에 발생하는 편향을 생각할 수 있다. 즉, 처치를 받은 학교와 처치를 받지 않은 학교는 태블릿에서만 차이가 있는 것이 아니라, 그 외 다양한 요인(수업료, 위치 등)에 차이가 있다.
떄문에 태블릿 제공이 학업 성적 향상에 도움이 된다고 이야기하기 위해서는 태블릿이 있는 학교와 없는 학교가 평균적으로 서로 비슷해야 한다.(비교가 가능해야 한다!)
아래는 이를 수식으로 증명하는 과정이다. (연관성은 $E[Y|T=1] - E[Y|T=0]$으로 측정, 인과관계는 $E[Y_1 - Y_0]$으로 측정)
전개의 과정을 하나씩 살펴보길 바란다.
$E[Y|T=1] - E[Y|T=0] = E[Y_1|T=1] - E[Y_0|T=0]$

그 최종 결과는 아래와 같다.

결론적으로 우리는 이 Bias를 없애야만 정확한 인과관계를 파악할 수 있는 것이다.
즉, 연관성을 인과관계와 같게 만들어주기 위해선 $E[Y_0|T=0] = E[Y_0|T=1]$이면 연관성은 인과관계와 같다고 볼 수 있다.
이 $E[Y_0|T=0] = E[Y_0|T=1]$ 수식은 단순한 수식이 아니라, 실험군과 대조군이 비교 가능하다는 것을 의미한다.
추가로, $E[Y|T=1] - E[Y|T=0] = E[Y_1-Y_0|T=1] = ATT$ 또한 처치받은 그룹과 처치받지 않은 그룹이 Treatment 자체에서만 다른 경우, $E[Y_0|T=0] = E[Y_0|T=1]$ 이고 인과효과는 처치를 받지 않은 그룹과 같다. 즉 이는 아래와 같은 수식으로 이해할 수 있다.

위와 같이 비교가능한 그룹인 경우에 두 집단의 평균차이가 인과효과가 된다.
만일, 실험군과 대조군이 동일(유사)한 경우 $E[Y_1|T=0] = E[Y_1|T=1]$로도 표현할 수 있다. 이렇게 실험군과 대조군이 동일하면 처치 전에도 교환이 가능하며 처치 후에도 실험군과 대조군이 교환이 가능하다.
즉, $E[Y_1 - Y_0|T=1] = E[Y_1-Y_0|T=0]$ 및 $E[Y|T=1] - E[Y|T=0] = ATT = ATE$
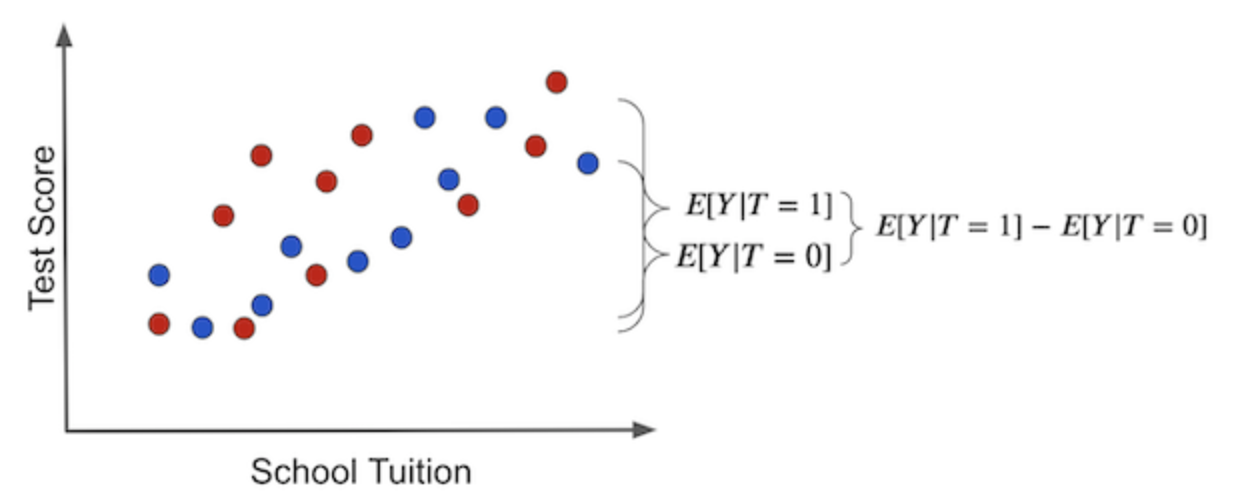
실험군과 대조군을 단순 평균에 대해 비교하면 아래와 같은 그래프를 얻을 수 있다. (파란색 점: 처치 X)

이 그래프에서 두가지 결과을 유추할 수 있다.
- Treatment Effect. 시험 점수 증가는 학생들에게 태블릿을 제공함으로써 발생한다.
- 시험 점수의 차이는 등록금 때문일 수 있다. 이 경우, 처치를 받은 학생들의 수업료가 더 비싸기 때문에 실험군과 대조군에서 차이가 생긴다. 때문에, Treatment가 성적의 증가를 유발하는 원인이 아니다.
ITE는 동일한 실험 대상에 대한 결과와 다른 대안의 처치를 받았을 경우, 얻을 수 있는 이론적 결과 간의 차이다. 실제 처치 효과는 사실상 얻을 수 없으며, 아래 왼쪽 그림과 같이 (예시로)예측한다. 이는 반사실 결과(Counterfactual Outcomes)이며 밝은 색으로 표시된다.
오른쪽 그래프에서는 bias를 나타냈다. 실험에 참가한 모든 대상이 처치를 받지 않는다면, $T_0$의 잠재적 결과만 남게된다. 그런 다음 처치된 그룹과 처치되지 않은 그룹의 차이를 확인한다. 만약 이런 상황에서 차이가 발생한다면 Treatment 이외의 다른 요인이 실험군과 대조군을 다르게 만드는 원인이 존재할 것이다. 이것이 바로 Bias며 Treatment에 대한 실질적인 효과를 가리게 된다.

Bias가 없는 상황과 대조해보도록 하자. 태블릿이 학교에 무작위로 할당된다면, 부유한 학교와 가난한 학교가 태블릿을 받을 기회는 동일하다.
이경우 처치를 받은 그룹과 받지 않은 그룹의 차이는 평균 인과 효과에 해당한다. Treatment 이외에 처치받은 그룹과 받지않은 그룹 사이에 다른 원인이 없기 때문이다. 즉 이런 경우엔 Bias가 없다. (즉, 태블릿이 모든 학생에게 고르게 분배가 되었다!)

이는 한 인과추론의 예시일뿐 우리가 알아야 하는 최종적인 과제는 아래와 같다.
- Bias를 제거하고 실험군과 대조군을 비교가능하게 하는 방법을 찾는다.
- 모든 차이가 평균적인 처리 효과(ATE)만으로 추청할 수 있게끔한다.
Reference
https://matheusfacure.github.io/python-causality-handbook/01-Introduction-To-Causality.html
01 - Introduction To Causality — Causal Inference for the Brave and True
matheusfacure.github.io
'Analytics' 카테고리의 다른 글
| [논문 리뷰] Prophet 시계열 예측 (0) | 2024.08.20 |
|---|---|
| [ML/DL] Long Short-Term Memory(LSTM) (0) | 2024.08.15 |
| [ML/DL] Recurrent Neural Network(RNN) (0) | 2024.08.09 |
| [NLP] Text Representation (0) | 2024.06.14 |
| [ML/DL] 인공 신경망(Neural Networks) (0) | 2024.05.10 |

