오늘은 Facebook에서 만든 시계열 예측 라이브러리인 Prophet을 리뷰해보려고 한다.
Introduction
논문에서 제시하는 실무에서의 비즈니스 예측 문제는 크게 아래 2가지이다.
- 완전히 자동화되는 시계열 예측 테크닉은 tuning하기 어렵고 유용한 가정이나 경험적인 사실들을 반영하기가 어렵다.
- 분석자는 도메인 지식은 풍부하지만, 시계열 예측에 대해서는 잘 알지 못한다.
위의 2가지 이유로 해당 논문에서는 아래 3가지 사항을 만족하는 시계열 모델을 만드는 것을 목표로 한다.
- 첫 번째, 시계열 방법에 대한 교육을 받지 않은 비전문가도 사용할 수 있어야 함.
- 두 번째, 잠재적 특징들을 시계열 모델에 반영할 수 있어야 함.
- 세 번째, 예측을 평가하고 다양하게 비교되도록 자동화 되어야 함.

많은 자동화 된 패키지와 마찬가지로 위 analyst-in-the-loop의 밑의 automated 파트는 자동화된 툴을 사용하는 것을 추구한다. 그리고 이러한 자동화된 패키지 구성에 더하여 시계열에서는 다양한 요소들이 고려되어야 한다.
Features of Business Time Series
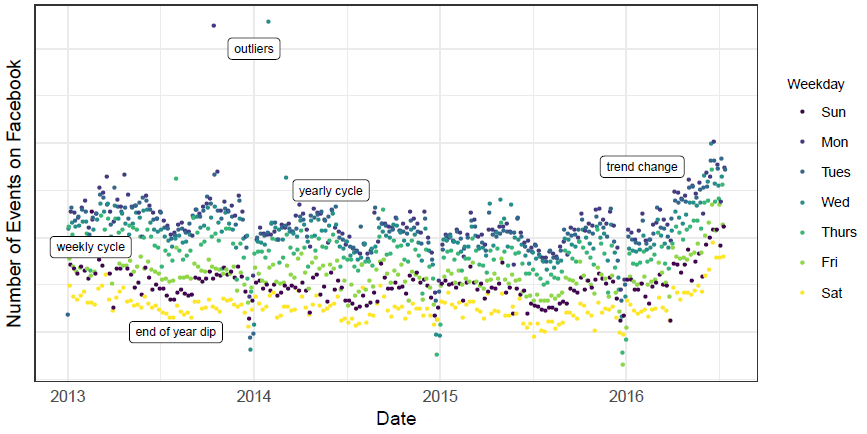
비즈니스 예측의 문제는 다양하지만, 공통적인 몇 가지 특징들이 존재한다. 아래는 페이스북에서 생성된 이벤트 수에 대한 시계열 데이터이다. 해당 데이터에서는 시계열 데이터가 가질 수 있는 계절적 요소를 확인할 수 있다. 주간 or 연간의 주기성이나 새해 직전에 잠깐 하강하는 모습이 있거나 최근 6개월 동안 과거와 달리 과도하게 변화하는 양상을 보이는 것을 확인할 수 있다. 이러한 움직임은 시계열 데이터에서 많이 보이고 완전히 자동화된 방법으로는 이런 데이터를 예측하는 것에는 한계가 있다.
아래 그림들은 Prophet 등장 이전에 완전히 자동화된 방법들의 한계를 보여주는 예측 결과다. auto arima, 지수평활법(ets), seasonal naive(snaive), tbats의 기법들의 예시들을 보여주며, 해당 모델들을 가지고 적절하게 조정하기 위해선 각 시계열 모델이 어떻게 작동하는지 철저히 이해해야 하는데, 일반적인 분석가들은 이러한 예측을 하지 못할 것이며 분석 및 예측이 잘못되고 있음을 지적한다.

The Prophet Forecasting Model
Prophet의 모형은 트렌드(growth), 계절성(seasonality), 휴일(holidays)의 3가지의 main components로 이루어진다.

- $g(t)$: 비주기적 변화를 반영하는 추세 함수
- $s(t)$: 주기적인 변화(ex. 주간/연간)
- $h(t)$: 휴일(불규칙 이벤트)의 영향력
- 모형이 설명하지 못하는 오차항($e_t$는 정규분포를 가정한다)
위의 구성은 일반화 가법 모형(GAM, generalized additive model)과 비슷하기 때문에, 새로운 요소를 추가하기가 쉽다.
쉽게 말하자면, 새로운 시계열 모델에 대해 쉽게 훈련할 수 있으며, 여러 기간에 대해 예측할 수 있다는 장점을 가진다.
Prophet은 다른 시계열 모형과 달리 시간에 종속적인 구조를 가지지 않고 Curve-fitting으로 예측 문제를 해결한다. 즉, 주어진 시계열 데이터의 패턴(추세, 계절성 등)을 잘 반영하는 수학적 곡선을 찾아내어 미래의 값을 예측한다. 이러한 방식을 통해 아래와 같은 이점을 얻을 수 있다.
- 유연성: 계절적 요소와 트렌드에 대한 가정을 쉽게 반영할 수 있다.
- ARIMA 모델과 달리 모델의 측정 간격을 Regularly spaced 할 필요가 없으며, 결측이 있어도 상관없다.
- 빠른 fitting 속도: 여러 가지 시도를 가능하게 한다.
- 직관적인 파라미터 조정
$g(t)$: Growth
페이스북에서 사용하는 trend model은 크게 두가지가 존재하는데, 상한/하한과 같은 한계점이 존재하는 saturating growth model과 두 번째는 상한/하한이 존재하지 않는 piecewise linear model과 piecewise logistic model의 경우다.
Saturating Growth

위의 그래프 처럼 예측하고자 하는 값에 대한 한계가 존재하는 경우에 우리는 그 한계를 반영한 모델을 세워야 한다.
Growth Forecasting이란, 특정 시계열 데이터와 관련된 population과 관련된 개념으로 페이스북에서 잠재적인 사용자 수가 증가해왔고 이후에 어떻게 증가할 것인지를 예측하는 것이다. 이를 nonlinear growth that saturates at a carrying capacity라고 부르는데, 이렇게 상한과 하한이 존재하는 growth는 아래와 같이 로지스틱 함수로 나타내진다. 페이스북에서의 Carrying capacity는 인터넷 접속이 가능한 사용자로 설정하고 있고 아래와 같이 $g(t)$를 정의하고 있다.

- $C$: 한계를 나타내는 carrying capacity
- $k$: 성장률(growth rate)
- $m$: offset parameter
piecewise logistic model
그러나 $C$와 $k$가 상수가 아니라 계속 변화하기 때문에, 이도 time에 따른 변화를 반영해야 한다.
이 문제를 해결하기 위해서 위의 Basic한 로지스틱 함수($g(t)$)에서 $C$를 시간에 따라 변하는 $C(t)$함수로 바꾸고 Change points 전후로 달라지는 성장률을 나타내기 위해 $k + a(t)^t$δ로 대체한 piecewise logistic growth model을 사용한다. 그 식은 아래와 같다.
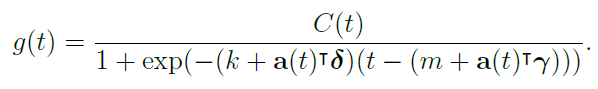
piecewise linear model
추가로, 앞의 경우와 달리 한계가 존재하지 않는 예측 문제에 있어서 piecewise linear 모델은 간결하고 유용하다.

논문에서는 아래와 같이 piecewise 하게 일정한 성장률을 가지는 trend model을 정의한다.
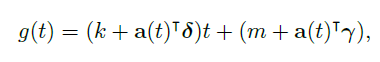
여기서 change points는 자동 탐지되고, 실제 적용 시 정도를 설정해 줄 수 있다.
$s(t)$: Seasonality
시계열 데이터는 인간 행동에 의해서 주기성을 가질 수 있다. 예를 들어 주 5일제는 주간 시계열에 영향을 주며, 방학은 연간 반복이 되어 영향을 준다. 이러한 주기성을 시계열 모델에 반영하기 위해 Seasonality 모델이 필요하다.
Seasonality 모델은 아래와 같이 푸리에 급수를 이용해 정의한다.

$P$는 시계열 모델에서 기대하는 정규 주기를 의미한다. (ex. $P$ = 7은 주간 데이터를 의미) 계절성 모델을 적합하기 위해서는 $2N$만큼의 parameter, $B = [a_1 + b_1 +, ..., a_N, b_N]^t$를 추정해야 한다.$N$은 계절성의 low-pass filter의 기능을 하고 그 값이 커질수록 모델은 패턴을 더욱 세세하게 감지한다.

(N값은 통상적으로 년 단위는 10, 주 단위는 3으로 설정하는 것이 가장 좋다고 한다.)
$h(t)$: Holidays and Events
휴일, 이벤트들은 산업 현장의 시계열에 많은 영향(ex. 추수감사절, 추석)을 준다. 그러나, 주기적인 패턴을 따르지 않기 때문에 모델링이 어렵다. 그러나 음력 행사나 추수 감사절(11월 4번째 목요일)과 같은 비주기적인 휴일들이 시계열에 미치는 영향은 매년 비슷하기 때문에 모델에 반영이 되어야 한다. 여기서 이벤트의 효과는 독립이라고 가정하고 이벤트 앞뒤로 window의 범위를 지정해 해당 이벤트의 영향력 범위를 설정할 수 있다.
각각의 holiday를 $D_i$로 명시하고 holiday i동안의 t와 각 휴일에 할당되는 파라미터를 $k_i$라고 했을 때, 아래와 같은 matrix를 만들 수 있다.

그리고 이를 계절성과 유사하게 아래와 같이 정의한다.


(한국의 휴일의 경우, Python의 holidays라는 패키지에 정의되어 있다.)
Model Fitting & Evaluating
지정된 time 길이에 맞춰 Model Fitting을 했다면, 모델이 잘 작동하는지 확인해봐야 하는데, 그 기준인 Accuracy는 아래와 같이 측정한다.
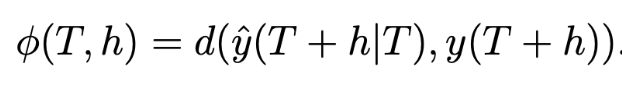
- $h$: 예측을 진행하는 기간
- $y(t|T)$: time T 이전까지의 정보를 이용해 time t에 대해 예측한 값 (여기서 y는 y_hat을 의미, 표기법을 못찾음)
- $d(y, y^,) = |y - y^,|$
그리고 이 때 아래의 error term은 몇가지 가정을 거친다.

- 연속된 time에서는 유사한 mistake가 생기는 것을 가정했기 때문에, h동안 error는 locally smooth해야 함.
- 시간이 지날수록 예측력은 떨어짐.
아래 두 사진은 각각 prophet을 이용하여 이전 다양한 모델들로 분석한 데이터와 동일한 범위를 예측하고 전체 데이터로 모든 시간에 대해 예측한 결과다. prophet의 결과가 다른 시계열 방법보다 주 단위, 연 단위 주기성을 더 잘 포착하고 있는 것을 파악할 수 있다.


더불어 prophet은 분해가 가능한 모델이기 때문에, 각 예측의 구성요소들을 아래와 같이 확인할 수 있으며 이를 통해서 예측 문제에 대해 다양한 통찰력을 얻을 수 있을 것이라 기대한다.

Reference
https://peerj.com/preprints/3190.pdf
https://facebook.github.io/prophet/docs/quick_start.html
Quick Start
Prophet is a forecasting procedure implemented in R and Python. It is fast and provides completely automated forecasts that can be tuned by hand by data scientists and analysts.
facebook.github.io
'Analytics' 카테고리의 다른 글
| [보충 리뷰] SHAP (3) | 2024.08.28 |
|---|---|
| [논문 리뷰] SHAP (1) | 2024.08.26 |
| [ML/DL] Long Short-Term Memory(LSTM) (0) | 2024.08.15 |
| [Causal Inference] Causal Inference for The Brave and True 리뷰 (0) | 2024.08.12 |
| [ML/DL] Recurrent Neural Network(RNN) (0) | 2024.08.09 |

