[논문 리뷰] SHAP

오늘은 설명가능한 AI에 대표적인 방법론인 SHAP 논문을 리뷰하려고 한다.

 

Abstract

 

인공지능에서 모델이 예측한 결과를 이해하는 것은 중요하다. 그러나, 앙상블과 딥러닝 같은 복잡한 모델을 사용함으로써 large modern dataset에서 높은 정확도를 보이는 경우에는 정확도와 해석력 사이에 tention이 발생한다.

 

많은 방법론들은 복잡한 모델의 예측을 설명하기 위해 제안되고 있지만, 이러한 방법론들이 어떻게 연관되어 있고 한 방법론이 다른 방법론에 대해 언제 더 선호되는지에 대해 아직 명확하지 않는다. 때문에 해당 논몬에서는 SHAP 방법론을 제안한다. SHAP은 각각의 Feature에 특정한 예측에 대한 중요도(기여도)를 부여한 값이다.

 

SHAP의 새로운 구성요소는 아래와 같다.

• The identification of a new class of additive feature importance measures
• Theoretical results showing there is a unique solution in this class with a set of desirable properties

 

Introduction

 

모델의 예측결과를 정확히 설명하는 능력은 사용자 신뢰를 만들고 모델의 향상에 대한 통찰력을 제공하는 등의 관점에서 매우 중요하다. 일부에서는 선형회귀 같은 단순한 모델들이 해석에 쉽다는 이유로 선호된다. 그러나 빅데이터의 성장은 복잡한 모델의 효과를 증가시켰고 모델결과의 정확도와 해석력 사이의 trade-off의 균형을 찾아야한다.

 

여기서 SHAP은 모델 예측을 설명하는 것에 대한 접근법을 통합했다. 이 접근법은 3가지의 중요한 결과를 제시한다.

1. 모델 예측에 대한 어떠한 설명도 보여주는 관점을 소개하며, 이것을 explanation model이라고 한다. 이것은 우리가 6가지 기존의 방법론들을 통합한 additive feature attribution methods를 정의하도록 만든다. (Section 2)
2. 게임이론을 바탕으로 additive feature attribution method의 전체 클래스에 적용하는 유일해를 증명한다. (Section 3) 다양한 방법들이 근사하는 feature importance의 통합된 척도로 SHAP 값을 제안한다. (Section 4)
3. 새로운 SHAP 값 추정 방법을 제안하고 이 방법들이 인간의 직관에 더 잘 일치하고 기존 방법들보다 모델 출력 클래스 간의 차이를 더 효과적으로 구별함을 입증한다. (Section 5)

 

Additive Feature Attribution Methods

 

단순한 모델은 이해하기 쉽다. 그러나 복잡한 모델은 이해하기 어렵기 때문에 일반적인 설명으로 모델을 사용할 수 없다. 그 대신 원래 모델을 해석가능한 방식으로 근사한 explanation model을 사용한다. 앞으로 등장하는 6가지 현재 설명 방법들은 모두 explanation model을 사용한다는 것을 보여준다. 

 

해당 논문은 explanation model의 additive feature attribution methods를 제안하는데 아래는 미리 정의해야 할 notation이다.

• $f$: 설명이 필요한 원래 모델
• $g$: $f$를 설명하기 위해 단순화된 Explanation model
• $x$: $f$에 들어가는 원래 input ($f(x)$는 원래 인풋에 대한 output)
• $x'$: $g$의 input으로 들어가는 $x$의 단순화된 형태
• $h_x$: $x'$을 $x$로 매핑하는 함수

 

Definition 1

 

Additive feature attribution methods는 이진 변수의 선형 함수에 대한 설명 모델이다.

(1)번 수식

• $z'$ ∈ ${0,1}^M$
  • M은 단순화된 입력 특성의 개수,ϕ$_i$ ∈ $R$
    
• $z'$은 0 또는 1 (이진 변수)
• Definition 1을 만족하는 설명 모델을 갖는 방식은 각 특성에 중요도(effect) ϕ$_i$를 부여하고 모든 특성의 중요도를 원본 모델의 출력 $f(x)$에 근사한다.

 

많은 기존 방식은 Definition1을 만족하는데, 아래에서 이에 대해 설명한다.

 

LIME

 

LIME은 주어진 예측 주변에 대해 지역적으로 근사한 모델에 기반하여 각 모델 예측을 해석하는 방법이다. LIME이 사용하는 local linear explantion은 (1)번 수식을 정확히 준수하기에 additive feature attribution method이다. 

LIME에서 $x'$는 해석 가능한 입력이라고 하고 매핑 $x=h_x(x')$은 interpretable inputs의 바이너리 벡터를 원본 입력 공간으로 변환한다. 서로 다른 입력 공간에 대해선 서로 다른 입력 형태의 $h_x$ 매핑이 사용된다.

 

ϕ를 찾기 위해 LIME은 아래와 같은 목적함수를 최소화 한다.

(2)번 수식

(자세한 설명은 생략)

 

DeepLIFT

 

DeepLIFT는 재귀적 예측 설명 방법이다. 이 방법은 각 입력 $x_i$에 원래 값을 대신하여 참조 값을 사용했을 때 효과를 나타내는 값 CΔxiΔy를 할당한다. DeepLIFT에서 매핑 $x = h_x(x')$은 이진 값을 원본 입력으로 변한하는데, 1은 원래 값을 취하는 것을 의미하고 0은 참조값을 취하는 것을 의미한다.

(3)번 수식

• $o = f(x)$: 모델의 출력
• Δ$o$ = $f(x) - f(r)
• Δ$x_i$ = $x_i - r_i$
  • $r$: 참조값

ϕi=CΔxiΔoϕi=CΔxiΔo, ϕ0=f(r)ϕ0=f(r)이라고 하면, 아래 수식과 같이 DeepLIFT의 설명 모델은 (1)번 수식과 일치하며, 또 다른 additive feature attribution method가 됩니다.

 

Layer-Wise Relevance Propagation

 

Later-Wise Relevance Propagation은 심층 신경망의 예측을 해석하는 방법이다. 이 방법은 모든 뉴런의 reference activations가 0으로 고정된 DeepLIFT와 동일하다.

 

Classic Shapley Value Estimation

 

위 세가지 방법은 전통적인 방정식을 사용한 방법이라면, Shapley regression values는 다중공선성이 존재하는 선형 모델의 Feature importance이다. 이 방법을 사용하기 위해서 모든 특성(Features)의 하위 집합 S⊆F에 대해 모델을 재학습해야 한다. (F는 모든 feature의 집합) 각 특성에 해당 특성을 포함하였을 때 모델 예측에 주는 영향을 나타내는 중요도를 할당한다. 이 영향을 계산하기 위해서 모델 $f_{SU{{i}}}$는 그 특성을 포함하여 훈련되고, $f_s$는 해당 특성을 제외하고 훈련한다. 그리고 현재 입력에 대하여 두 모델의 예측을 비교하는데, 이를 $f_{SUi}(x_{SUi})-f_s(x_s)$와 같이 나타낸다. ($x_s$는 집합 S에 있는 입력 특성들의 값)

(4)번 수식

 

즉, ϕ$_i$는 Feature $i$를 제외한 $F\{i}$의 모든 집합에서 $i$를 추가했을 때 output의 변화량의 평균을 측정한 값이다.

 

Simple Properties Uniquely Determine Additive Feature Attributions

 

Addictive Feature attribution methods는 유일해를 가진다. 그리고 Addictive Feature attribution methods가 유일해를 가질 조건은 아래와 같다.

 

Property 1: Local accuracy

 

(5)번 수식

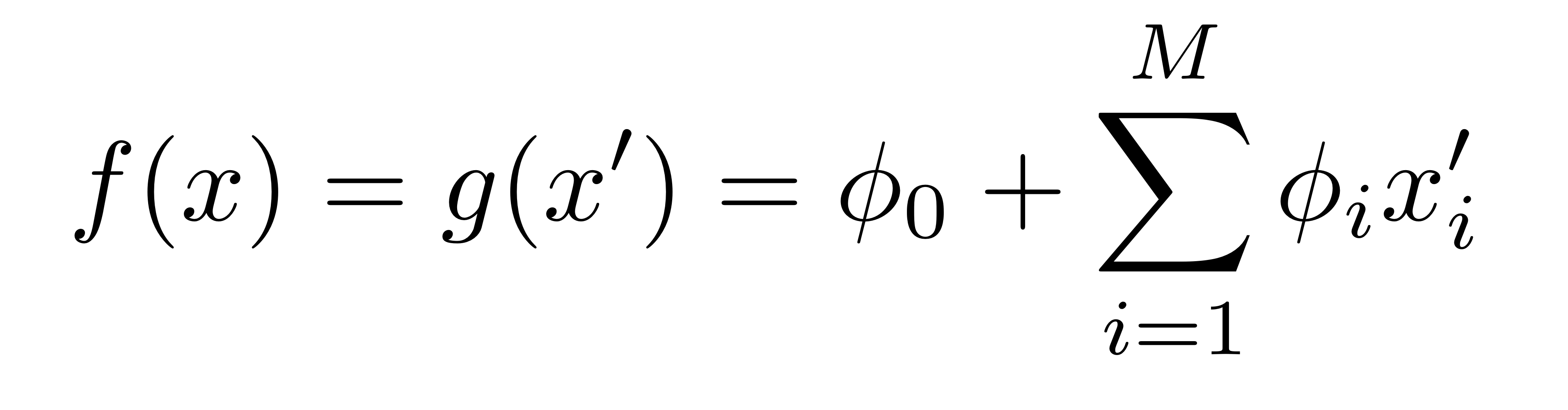
explanation model인 $g(x')$은 $x = h_x(x')$의 조건하에서 $f(x)$와 매칭된다.

즉, 원래 모델 $f$로부터 생성된 output인 $f(x)$를 설명하기 위한 $g$가 Local accuracy를 만족해야한다.

 

Property 2: Missingness

 

(6)번 수식

단순화된 input인 $x'$에서 Feature $i$에 해당하는 값이 0이라면 해당 변수의 영향력(ϕ)도 0이라는 것이다.

 

Property 3: Consistency

 

(7)번 수식

 

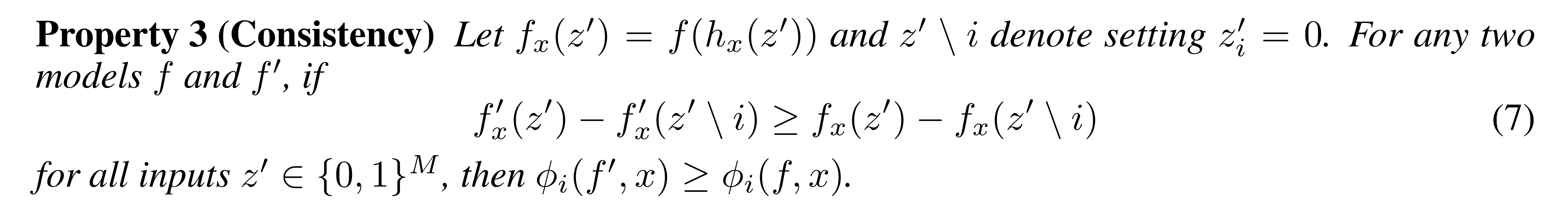
만약 모델이 $f$에서 $f'$으로 바뀌었을 때, Feature i의 영향력이 더 커지면, $f'(x)$의 Explanation model의 Feature i에 대한 계수가 $f(x)$보다 더 크다는 것이다.

---

 

Theorem 1

 

위 세가지 Property가 성립될 때, 아래와 같은 정리가 도출된다.

(8)번 수식

 

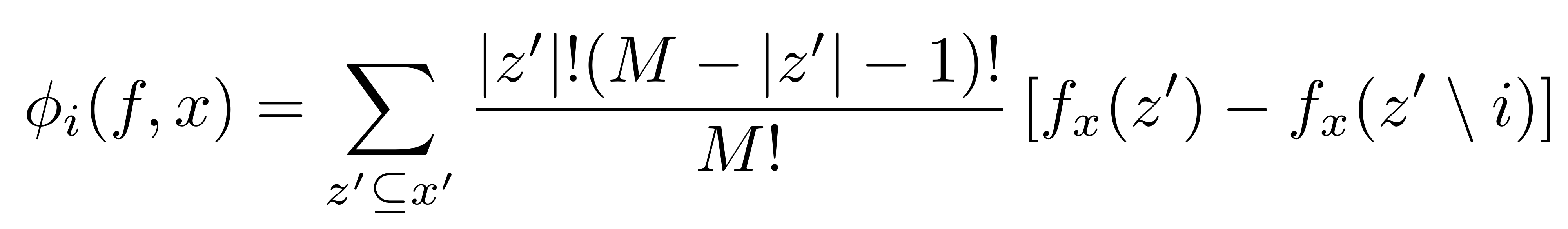
즉, Property 1, 2, 3을 만족할 때, Additive feature attribute methods을 통해 나온 Explanation model $g$는 오직 하나 존재한다.

 

SHAP (SHapley Additive exPlanation) Values

 

SHAP 값이 계산되는 방법은 다음과 같다.

• $z' $  ∈ ${0, 1}^M$과 $z'$의 non-zero index의 집합 S를 정의
• $f_x(z') = f(h_x(z')) = E[f(z)|z_s]로 두고 Theorem1의 (8)번 수식의 해 산출

 

단순화된 $z'$로부터 Shapley value를 구하면 되는 것인데, 이 과정은 $2^{|S|}$의 시간복잡도를 갖기 때문에, 정확한 SHAP value를 찾는 것이 매우 어렵다고 한다. 논문에서는 이에 대해 additive feature attribution methods를 활용하여 근사치를 얻을 수 있다고 하는데, 하나는 Shapley sampling values고 다른 하나는 Kernel SHAP이라는 방법이다. 더불어 모델에 따라 다르게 적용할 수 있는 네가지 근사법을 소개했는데, 그 중 두 개는 Max SHAP과 Deep SHAP이다. (여기서는 Kernel SHAP만 살펴본다.)

 

Kernel SHAP (Linear LIME + Shapley values)

 

LIME은 아래 식을 사용하여 Explanation model $g$를 산출한다.

(2)번 수식

 

여기에선 손실함수 $L$, 인스턴스 간의 거리에 대한 커널인 π,  정규화 식인 Ω를 어떤 것으로 설정하느냐에 따라 산출하는 Explanation model이 달라지게 된다. 그리고 Explanation model로 선형식을 쓰는 경우의 LIME은 본 논문에서 정의했던 Additive feature attribution methods에 속하기 때문에, 만약 Additiive feature attribution methods가 오직 하나의 해를 갖기 위한 조건인 Property 1~3을 따른다면, Theorem 1에 의해서 Explanation model의 각 변수들에 대한 계수는 Shapley value를 따르게 된다.

때문에 필요한 작업은 Property 1~3을 만족하는 $L$ ,π, Ω 를 결정하는 것이다. 여기에서는 Theorem 2에서 이를 만족하는 Shapley Kernel을 제시합니다.

 

Theorem 2 (Shapley Kernel)  Definition 1에서, 다음을 만족하는 $L$,π$_{x'}$,Ω는 (2)번 식이 Property 1~3을 만족하게 한다.

 

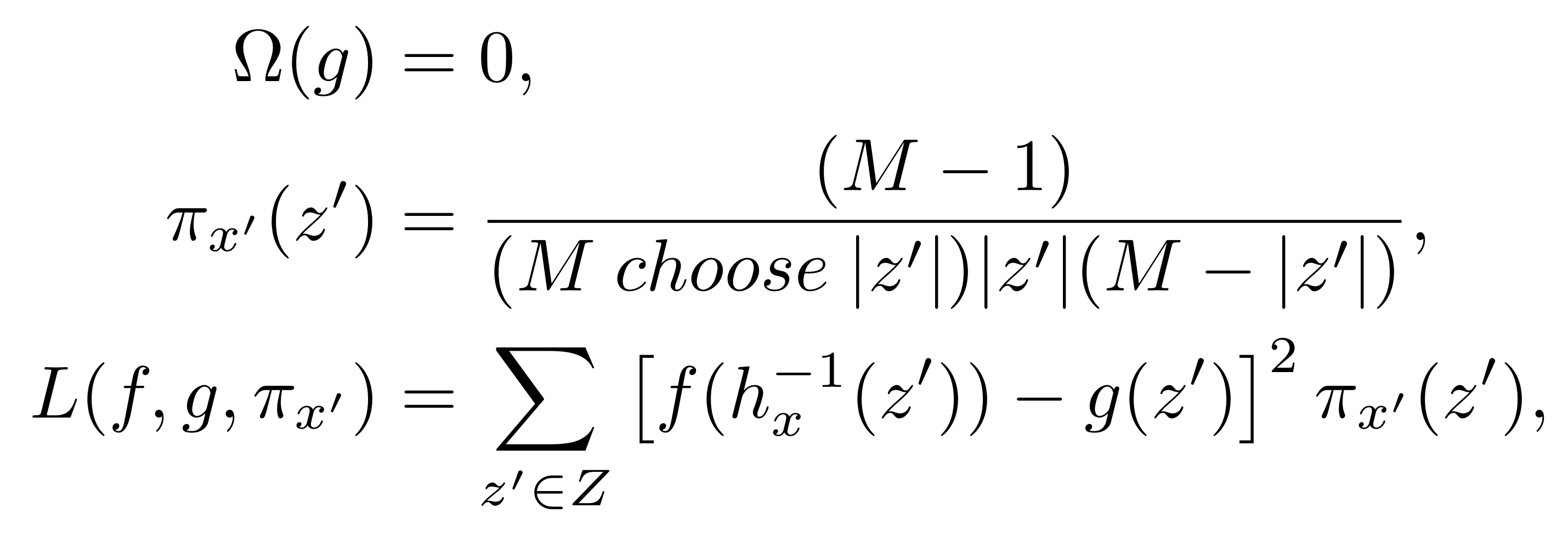
Theorem 2에서 제시하는 $L$ ,π, Ω를 만족한다면, LIME을 수행했을 때 산출되는 선형 Explanation model의 계수들이 Shapley value와 일치한다는 것이다.

 

---

Reference

https://arxiv.org/abs/1705.07874

A Unified Approach to Interpreting Model Predictions

https://kicarussays.tistory.com/32

[논문리뷰/설명] SHAP: A Unified Approach to Interpreting Model Predictions

https://basicdl.tistory.com/entry/%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0-A-Unified-Approach-to-Interpreting-ModelPredictions

[논문리뷰] A Unified Approach to Interpreting Model Predictions