최근 SHAP 논문을 리뷰해보았는데, 읽었음에도 불구하고 이해가 잘 되지 않는 부분이 많아서 강의를 통해 다시 한번 정리하고자 한다.
Introduction
최근 딥러닝 모델이 복잡해짐에 따라 예측성능이 향상되고 있는데, 예측 성능이 높아지는 것은 고무적인 현상이지만 네트워크가 너무 복잡해지기 때문에 그 과정(Process)이 설명이 되지 않는 현상들이 발생한다.


예측 결과도 좋으면서 그 과정을 설명까지 할 수 있다면, 굉장히 좋은 모델링이 될 수 있을 것이다. 최근에 설명가능한 인공지능 XAI에 대한 방법론들이 많이 등장하고 있는데, 그 중 대표적인 것이 바로 SHAP 방법론이다.
Shapley addictive explanation (SHAP) 개념 소개
(SHAP은 게임 이론에 기반을 두는데 게임이론은 몰라도 된다.)
예제를 통해 SHAP을 이해해보자.
민철, 은영, 지연, 지호 4명이 서로 머리를 맞대어 시험을 보았고 점수는 100점이라고 하자.
이틀 후에 같은 수준의 시험을 봤는데, 민철이가 빠지고 은영, 지연, 지호 3명만 시험을 보았는데 점수는 20점.
이후 같은 수준의 시험을 은영이만 빠지고 민철, 지연, 지호만 보았는데 점수는 80점.
이후 같은 수준의 시험을 지연이만 빠지고 민철, 은영, 지호만 보았는데 점수는 70점.
이후 같은 수준의 시험을 지호만 빠지고 민철, 은영, 지연이 보았는데 점수는 99점.
이라고 하자. 이러한 상황에서 민철, 은영, 지연, 지호 중 시험을 잘 보는데 가장 큰 기여를 한 사람은??
이러한 상황에 직관적으로 시험에 많은 기여를 한 사람을 민철, 가장 적은 기여를 한 사람은 지호라는 것을 알 수 있다.
Shepley value의 기본 개념은 전체가 다 있을 때 대비 어떤 구성원 하나가 빠졌을 때의 점수 차이를 비교하면서 그것을 보고 중요한 역할을 결정하는 하는 변수를 결정하는 것이다.
Shapley addictive explanation (SHAP) - Example

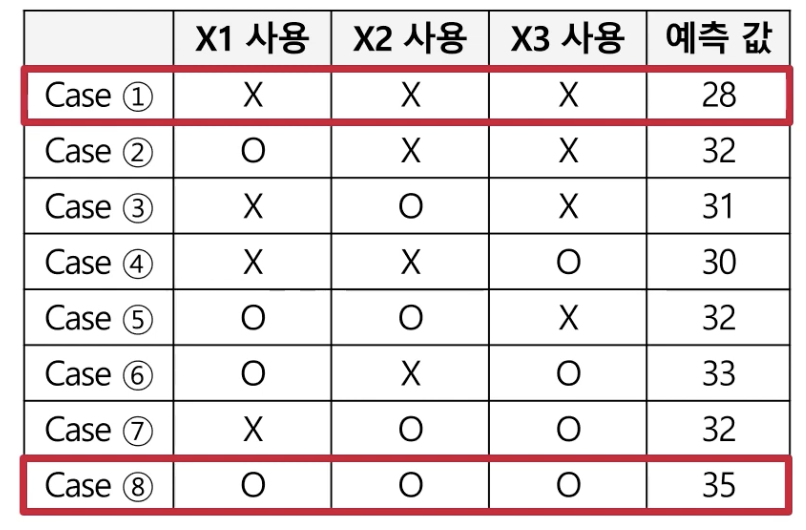
예를 들어 Shapley value 계산 방법을 알아보자. (새로운 관측치의 X1 변수에 대한 Shapley Value 계산 방법)
위의 입력 변수는 X1, X2, X3이며, X1 변수를 예측에 사용하는지 여부에 따라 예측값을 비교하는 것이 핵심이다.
- X1만 사용했을 때
- $case2 - case1 = 32 - 28 = 4$
- X1를 포함하여 변수 2개를 사용했을 때
- $case5 - case3 = 32 - 31 = 1$
- $case6 - case4 = 33 - 30 = 3$
- X1를 포함하여 변수 3개를 사용했을 때 (모든 변수 사용)
- $case8 - case7 = 35 - 32 = 3$
이때, X1에 대한 shapley value를 구할 때 가중치가 달라지게 된다.
- 변수를 1개만 사용하는 경우
- X1, X2, X3를 각각 사용하는 3가지 경우인데 X1이 제거가 가능한 경우는 1가지이다. 따라서 해당 가중치는 $1/3$이다.
- 변수를 2개만 사용하는 경우
- 변수를 2개만 사용하는 경우는 (X1, X2), (X2, X3), (X3, X1)의 3가지 경우이다.
- 이 때 두 변수 중 한 변수를 제외하는 경우는 2가지이므로 총 경우의 수는 6가지이다. 그리고 각각의 경우에서 X1변수를 제외할 수 있는 경우는 각각 1가지이기 때문에 해당 가중치는 $1/6$이다.
- 변수를 모두 사용하는 경우
- 변수 3개를 사용하는 경우는 1가지인데, 세 변수 중 한가지 변수를 제외하는 경우의 수는 X1, X2, X3를 제외하는 3가지이다. 그리고 그리고 그 중 X1를 제외하는 경우는 1가지이기 때문에 해당 가중치는 $1/3$이다.
즉, 이를 통합하여 X1에 대한 Shapley Value(=기여도)는 $4 * 1/3 + 1 * 1/6 + 3 * 1/6 + 3 * 1/3 = 3$임을 도출해낼 수 있다.
그리고 X2, X3에 대한 기야도를 구하면 아래와 같다.

흥미로운 점은 총 Shapley Value를 더한 값인 7이 Case 8 - Case 1을 한 값과 동일하다는 것이다.
실제로 논문은 위의 예시를 사용하지 않고 아래의 수식으로 Shapley value 계산 방식을 정리한다. 그러나 이는 관심 관측치마다 아래 계산이 필요하기 때문에, 연산량이 많다는 단점이 존재한다.

Shapley addictive explanation (SHAP) 그래프 해석하기
아래는 사망률-예측 정형 데이터에 대한 Shapley value 그래프이다.
- Age가 높을 수록 Shapley value가 높고 낮을 수록 낮다. => 나이가 사망률에 높은 기여를 함
- White blood cells이 높을 수록 Shapley value가 높다. => While blood cells가 사망률에 높은 기여를 함
- Blood protein은 전체 변수 중요도는 낮지만, 사망률을 높이기에 주의할 필요가 있다.
추가로 입력 변수 별 양수 Shapley value를 모두 더해 변수 중요도로 환산할 수 있다.

Shapley value 해석하기
이미지 분류 모델을 해석할 때도 Shapley value를 적용할 수 있다. 아래 그림에서 빨간색으로 표시된 영역이 Shapley value가 높은 부분이다. 여기서 새는 부리를 보고, 미어캣은 눈을 보고 각각을 예측함을 알 수 있다.

Shapley value 장/단점
- 장점
- LIME 방법론(local model)과 달리 모든 학습 데이터에 대한 예측 값을 기준으로 시작된다.
- 전체 데이터 중 관심 관측치의 위치를 파악하고 해석하는 것으로 이해가 가능하다.
- 정형 데이터의 경우, 관측치 별 해석과 전반적 변수 중요도 산출이 가능하다.
- 어떤 모델을 사용하던지 간에, 모델 결과가 나오면 어디든지 사용할 수 있다. (Model-Agnostic explanable AI)
- 딥러닝의 attention 개념도 중요도를 산출하는 것으로 볼 수 있는데, 그러나 attention은 Model-dependent 방법론이다.
- 단점
- 모든 순열에 대해 계산을 진행하기에 많은 시간이 소요된다.
- Shapley value는 모델 학습 후 산출하는 것으로 원인/결과(인과관계)로 생각해서는 안된다.
- 해당 변수가 예측에 중요한 변수는 맞지만, 그것이 원인이 되는 원수는 아니다는 것을 명심하자!
Reference
https://www.youtube.com/watch?v=f2XqxOny3NA
'Analytics' 카테고리의 다른 글
| [ML/DL] Seq2Seq with Attention (0) | 2024.09.02 |
|---|---|
| [ML/DL] Sequence to Sequence Learning with Neural Networks (1) | 2024.09.01 |
| [논문 리뷰] SHAP (1) | 2024.08.26 |
| [논문 리뷰] Prophet 시계열 예측 (0) | 2024.08.20 |
| [ML/DL] Long Short-Term Memory(LSTM) (0) | 2024.08.15 |

