오늘은 Seq2Seq에 이어 Attention 개념을 설명해보고자 한다.
seq2seq 모델에는 치명적인 단점이 존재한다. 만약, 입력 Sequence의 길이가 많이 길어지게 되면 한정된 길이의 Context Vector에 모든 입력 시퀸스의 정보를 담기가 상당히 어려워진다. 이러한 문제를 해결하기 위해 Attention 매커니즘이 활용된다.

Attention 매커니즘은 디코더가 출력 시퀸스의 단어들을 생성할 때, 입력 시퀸스의 어떤 부분이 중요한지를 주목(attention)하게 만드는 알고리즘이다. Attention 매커니즘은 모델이 훨씬 더 긴 시퀸스를 처리할 수 있게하고 번역 품질을 개선하는 등 여러 이점을 제공하며, 특히 복잡한 문장 구조나 먼 거리의 의존성을 가진 언어 작업에서 효과가 눈에 띄게 나타난다.

그렇다면, Attention 매커니즘이 어떻게 작동하는지 알아보자.
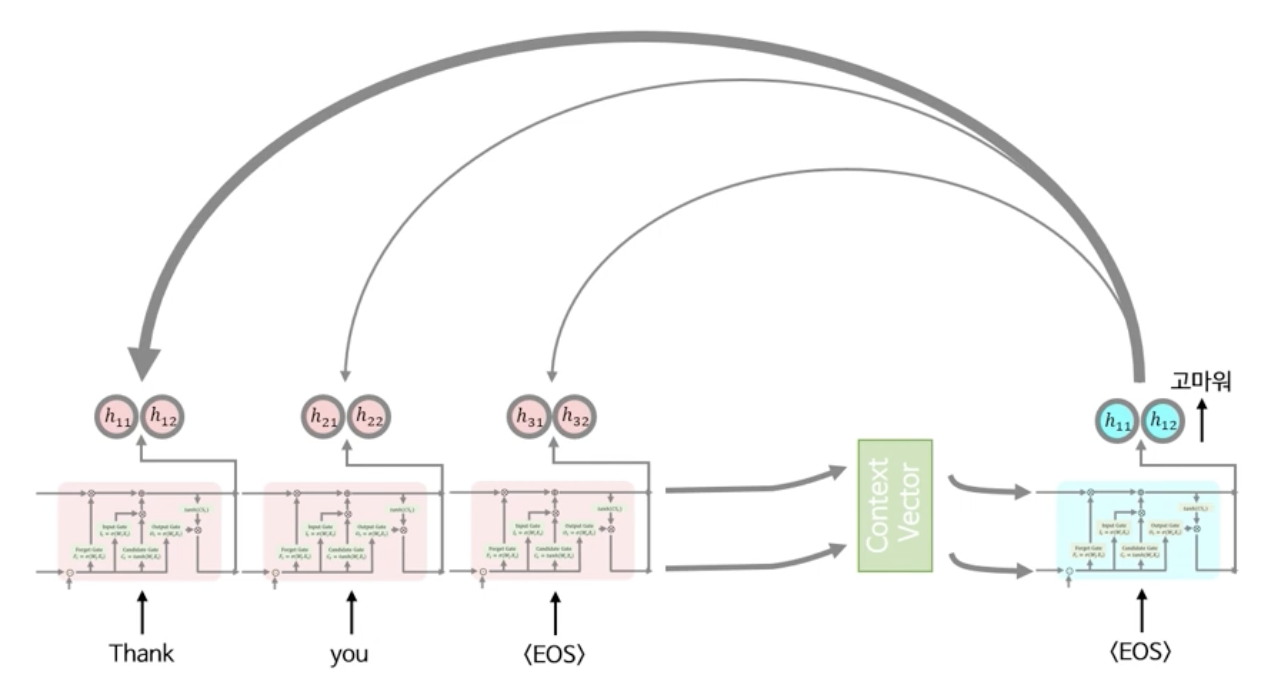
만약 아래와 같이 Thank, you, <EOS>와 같은 입력 시퀸스가 들어온다고 가정하게되면 입력 단어에 대한 각각의 Hidden State들$h_{11}, h_{12}, h_{21}, h_{22}, h_{31}, h_{32}$을 따로 저장해둔다. (동그라미 2개는 크기가 2인 벡터를 뜻한다고 가정하자)

그 다음 앞선 seq2seq에서의 설명과 마찬가지로, Context Vector를 만들고 디코더에 넣어서 디코더의 은닉상태($h_{11}, h_{12}$)와 출력값(고마워)를 구할 수 있게 된다.

Attention 매커니즘의 핵심은 현재 디코더 은닉상태와 가장 관련이 있는 것으로 추정되는 입력과의 관계성을 찾는 것인데, 이 때, 두 은닉상태의 관계성을 결정짓는 척도는 바로 두 벡터간의 유사성이다.
벡터간의 유사성을 계산하는 Attention 점수 계산법은 크게 아래 3가지 정도로 나뉘는데, 각각의 방법은 서로 다른 특징이 있고 복잡도가 다르지만, 결론적으로 입력 시퀸스와 출력 시퀸스 간의 벡터 유사성을 비교하는 관점에서의 효과는 비슷하다.
- Dot product
- Bilinear
- Multi-layer NN
(여기서는 Dot product 방법을 사용한다.)
다음과 같이 출력 시퀸스와 입력 시퀸스의 Hidden state의 Attention Score를 Dot product를 사용해 계산하여 구한다.
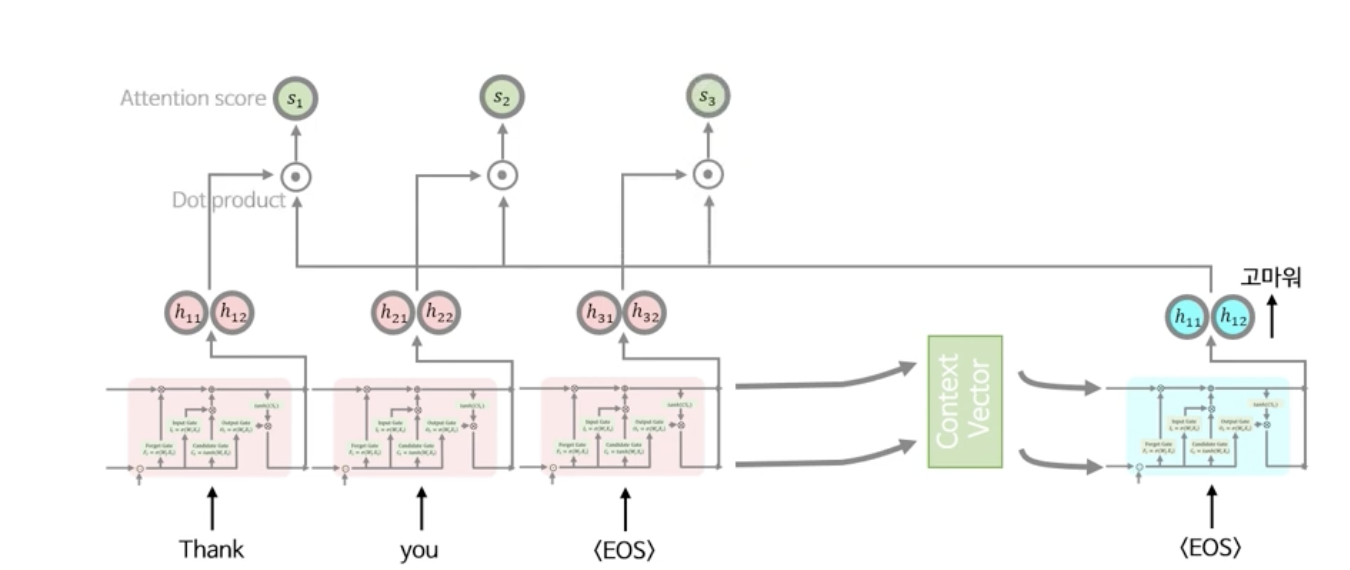
각 Attention Score를 구했으면, 그 Attention Score의 Softmax값을 구한다.
(Softmax를 취하는 이유는 각 Attention Score들을 확률분포로 바꾸고 정규화하여 학습을 효과적으로 하기 위함이다)

그 다음으로 각 Attention Score들과 기존의 입력 시퀸스들의 Hidden State 값들과 곱한다. Attention Score들은 간단한 스칼라값이기 때문에, 곱셈을 통해서 기존의 입력 시퀸스의 Hidden State들에게 Attention 가중치를 증폭해주는 효과가 있다고 생각하면 된다.

그 후 Attention Score가 추가된 입력 시퀸스의 Hidden State들을 다 더하여 새로운 Context Vector($C_1, C_2$)를 만들게 된다.

새롭게 만들어진 Context Vector는 기존에 있는 Context Vector에 비하여 Attention Score가 증폭된 새로운 Hidden State이기 때문에 다음번 디코더 LSTM의 Hidden State로 입력하고 차례로 필요한 값들을 입력하면 다음번 Hidden State $h_{21}, h_{22}$를 구할 수 있고 앞선 방법과 똑같은 방식으로 그 다음 턴의 Attention Context Vector를 구할 수 있게 된다. (원래 디코더의 출력이 <EOS>가 되면 Attention은 더 이상 계산할 필요가 없지만, 여기에서는 예시를 통해 구해본다)


Reference
https://www.youtube.com/watch?v=cu8ysaaNAh0&t=422s
'Analytics' 카테고리의 다른 글
| [Causal Inference] 유용한 선형회귀 (4) | 2024.09.18 |
|---|---|
| [Causal Inference] 인과추론 기초 & 무작위 실험 (16) | 2024.09.16 |
| [ML/DL] Sequence to Sequence Learning with Neural Networks (1) | 2024.09.01 |
| [보충 리뷰] SHAP (3) | 2024.08.28 |
| [논문 리뷰] SHAP (1) | 2024.08.26 |

